OFFICIAL/関連
TUTORIAL
TOPICS
ETC
EDIT
REFERENCE
LOG
お知らせ
HSP Web-Ring
最新の40件
2013-11-28
2013-11-25
2013-11-24
2013-11-23
2013-11-14
2013-11-13
2013-11-10
2013-11-06
2013-10-23
2013-10-21
2013-10-20
2013-10-15
2013-10-12
2013-10-06
2013-09-15
2013-08-28
2013-08-26
2013-08-15
2013-08-06
2013-08-05
2013-08-02
2013-07-05
2013-07-02
2013-06-29
2013-06-28
2013-06-27
2013-06-25
2013-06-14
2013-06-01
2013-05-29
2013-05-28
total: 2927
today: 1
yesterday: 1
now: 1
today: 1
yesterday: 1
now: 1
跳ねるボールその2 †
斜面との衝突を計算するにはベクトル演算が便利です。
以下、速度ベクトルをv,斜面の法線ベクトルをnとします。
斜面衝突時、速度ベクトルの斜面に垂直な成分は
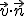
で表されます。
よって跳ね返り係数をe(<0)とすると、
Yvec{n}Yleft(~Yvec{v}~Ycdot~Yvec{n}~Yright).gif)
が衝突後の速度ベクトルとなります。


1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 | - | | | | - | | | | | | ! - | | ! - | | | | | | | | | | ! - | - | ! | |
Last-modified: 2007-04-08 (日) 02:48:27 (2436d)
Site admin: Charlotte
PukiWiki 1.4.7 Copyright © 2001-2006 PukiWiki Developers Team. License is GPL.
Based on "PukiWiki" 1.3 by yu-ji. Powered by PHP 5.3.27. HTML convert time: 0.064 sec.
Based on "PukiWiki" 1.3 by yu-ji. Powered by PHP 5.3.27. HTML convert time: 0.064 sec.