OFFICIAL/関連
TUTORIAL
TOPICS
ETC
EDIT
REFERENCE
LOG
お知らせ
HSP Web-Ring
最新の40件
today: 2
yesterday: 0
now: 1
三角関数 ![[hsp3]](./image/req/hsp3.png) †
†
HSP3から三角関数が標準で利用できるようになり、特にゲームの作成に威力を発揮するようになりました。
しかし三角関数は高等学校で学ぶため、小中学生プログラマにとっては理解が難しい壁となる可能性があります。
このページがそうした小中学生プログラマの助けとなれば幸いです。
1周を360°とする度数法に対し、円の半径と同じ長さの弧を切り取る2本の半径が成す角の値を1ラジアンとする角度の測り方を弧度法と言います。ラジアンとは角度の単位で、radと略されることや表記自体を省略することもあります。
度数法で言う360°は、弧度法では2πラジアンになります。π(パイ)は円周率のことで、3.1415...と無限に続く小数です。度とラジアンの間には、
(度)*π/180 = (ラジアン)
の比例関係があります。
三角関数を利用する際は、この弧度法を用いるのが普通です。HSPの関数でも弧度法を利用しています。最初は慣れないと思いますが、積極的に使って慣れてみてください。
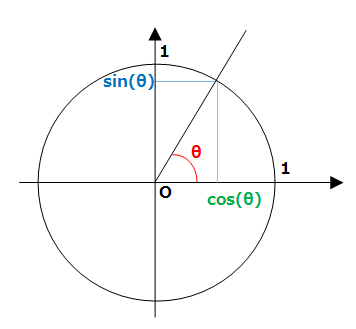
角度は水平右方向を基準(ゼロ)として、反時計まわりを正とします。
例えば真上(Y軸正の方向)は、基準である右方向から1周の4分の1だけ反時計まわりに進んだ角度なので、
- 90°
- -270°
- 450°
- π/2ラジアン
- -3π/2ラジアン
などと表現できます。
このように、角度は負の値や2πラジアン(360°)より大きい値をとることも可能です。
|
ゲームでは縦方向の速度を決定する時などに使います。正弦とも言います。 ゲームでは横方向の速度を決定する時などに使います。余弦とも言います。 正接とも言います。 角度から傾き*1を求めることができます*2。角度を指定して直線を引く時などに使えます。 タンジェントの取る値に制限はありません。負の無限大〜正の無限大の値をとります。 |
|
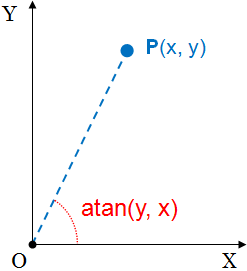
これは正確には三角関数ではなく、逆三角関数です。タンジェントの逆関数*3なのでそう呼ばれます。 本来は傾きから角度を求める関数ですが、HSPのatan関数はそれに加えて点のX座標とY座標から
を求める関数としても利用することができます(これらは表現が違うだけで同じものを表します)。書き方は以下のとおりです。
本来X座標がゼロの場合は傾きが定義されないので、atan関数の引数もまた定義されないはずです。 しかしHSPのatan関数はX座標がゼロの場合でも値を返すことができます。返す値は
です。 |
三角関数には他にもアークサインやアークコサインなど様々な種類があります*4が、通常使用することはないものばかりです。
上記4種の三角関数で十分足りるでしょう。
プログラム(ゲームが主になると思いますが)での利用方法を紹介します。
ストックのある方はぜひ追記をお願いいたします。
例えば標的に向かって進む弾(追跡弾)の場合、
- 弾を始点とした標的までの角度を調べる(atan関数)
- 調べた角度から、YおよびX方向の速さを決める(sin関数およびcos関数)
というステップで三角関数を使用することになります。
サインとコサインが-1〜1の値をとることは、弾速を決める際にとても便利です。なぜならば、
X方向の速さ = スピード * サイン Y方向の速さ = スピード * コサイン
で決定できるためです。
n-wayショット(n-way弾)や全方位発射の作成でも、sin関数とcos関数を使えば簡単なスクリプトで実現できます。
| + | sin&cosサンプル |
文字が円を描いて運動するサンプル
|
| + | tanサンプル |
角度を指定して直線を描くサンプル
|
| + | atanサンプルコード |
マウスで描いた直線とx軸との角度を表示するサンプル。
シューティング系のサンプルコードでよく使われているので、そちらも参照してください。 |
| + | sin&cos&atan複合サンプル |
星をくるくる回す。 左クリックのドラッグで回転、右クリックのドラッグ(上下)で拡大縮小
|
その他、新たにページを作るほどでもない、角度に関連する小技です。
| + | サンプルコード |
|
- atanのサンプル書いてみましたが、なんだかsinとか他のに比べて長くなってしまいました…。(-_-; -- GENKI? 2007-06-12 (火) 22:36:57
- おはようございます。理解しやすく、良いサンプルコードですね。勝手ながら不要なゼロ除算判定を行っている点など数点手を加えさせていただきました。
deglimitは新鮮でした![[bsmile2]](./image/face/bigsmile2.png) 追跡弾でも似たような処理があるので、今度書きなおしてみようと思います。 -- eller 2007-06-13 (水) 05:45:00
追跡弾でも似たような処理があるので、今度書きなおしてみようと思います。 -- eller 2007-06-13 (水) 05:45:00 ![[tere]](./image/face/tere.png)
![[sig]](./image/face/siguma.png) 修正ありがとうございます!atanの引数を勘違いしてました!
修正ありがとうございます!atanの引数を勘違いしてました! ![[sad2]](./image/face/sad2.png) 道理でおかしいと…。 -- GENKI? 2007-06-13 (水) 22:14:05
道理でおかしいと…。 -- GENKI? 2007-06-13 (水) 22:14:05- atanは引数の数によって振る舞いが変わり、傾きだけを渡すことも可能なので、勘違いではないですよ^-^;。 ただ、2つに分けて渡した方がゼロ除算判定が不要だったり戻り値の幅が広がったりして便利ですね。 -- eller 2007-06-14 (水) 08:15:00
- 三角関数についてはじめて知りました!あまり理解できなかったですが、レースゲームの進行方向とかに使えそうです、 -- カスタマー? 2009-06-19 (金) 18:14:13
- atanを使うと真上が-90・・・何この矛盾。。 -- 2010-07-22 (木) 00:00:36
- ↑今更自己解決 -- 2010-09-11 (土) 13:39:34
- 非常にわかりづらい -- 2011-01-06 (木) 04:01:45
- がんばります
![[hu]](./image/face/hu.png) -- あ? 2011-08-18 (木) 20:43:09
-- あ? 2011-08-18 (木) 20:43:09 - 初めまして。中学生ですがタンジェント、アークタンジェントがよくわからないです。 -- komaneko? 2011-10-31 (月) 22:14:23
- はじめまして。小学生なんですがatanを使いたいんですが -- sasaki? 2012-03-31 (土) 16:16:55
- ↑切れてしまってすいません。 -- sasaki? 2012-03-31 (土) 16:17:35
- atanを使いたいんですがよくわかんないです。です。失礼しました。 -- sasaki? 2012-03-31 (土) 16:18:24
- ゲーム感覚で -- 三角マン? 2012-07-13 (金) 22:07:57
- ゲーム感覚で三角関数学べませんか? -- 三角マン? 2012-07-13 (金) 22:08:54
*1 Yの変化量 / Xの変化量
*2 鉛直方向の傾きは定義されません
*3 関数y = f(x)が成り立つとき、x = g(y)となるg(y)をy = f(x)の逆関数と呼びます
*4 アークサインとアークコサインはhspmath.asで定義されています
Based on "PukiWiki" 1.3 by yu-ji. Powered by PHP 5.3.27. HTML convert time: 0.138 sec.